Giriş: Karar Ağacı Nedir?
Karar ağacı, bir dizi karar kuralını kullanarak verileri sınıflandırmak veya tahminlerde bulunmak için kullanılan güçlü ve popüler bir makine öğrenmesi algoritmasıdır. Adından da anlaşılacağı gibi, bir ağaç yapısı gibi görünür ve her düğüm bir take a look at veya karar noktasını temsil eder. Dallar, kararın olası sonuçlarını gösterir ve yapraklar ise son sınıflandırmayı veya tahmini temsil eder.
Basitliği ve yorumlanabilirliği, karar ağaçlarını hem yeni başlayanlar hem de uzmanlar için çekici kılar. Bir karar ağacına bakarak, modelin verileri nasıl sınıflandırdığını kolayca anlayabilir ve hangi özelliklerin önemli olduğunu görebiliriz.
Bu yazıda, karar ağaçlarının temel prensiplerini ve nasıl çalıştığını basit bir örnek üzerinden inceleyeceğiz. Öğrenci başarısını tahmin etme senaryosunu ele alacağız. Öğrencilerin ders çalışma alışkanlıklarını ve diğer faktörleri kullanarak, bir öğrencinin dersi geçip geçmeyeceğini tahmin etmeye çalışacağız. Bu süreçte, entropi ve bilgi kazancı gibi önemli kavramları ele alacak ve Python’da karar ağacının nasıl oluşturulacağını ve görselleştirileceğini adım adım göstereceğiz.
Veri Seti ve Özellikleri
Bu çalışmada, öğrenci başarısını etkileyebilecek faktörleri ve ders geçme durumunu içeren basit bir veri seti kullanacağız. Veri setimiz aşağıdaki gibi:
Bu veri setinde üç sütun bulunmaktadır:
- Öğrenci: Öğrencinin adı.
- Çalıştı mı?: Öğrencinin derse çalışıp çalışmadığını gösterir (Evet/Hayır).
- Dersi Geçti mi?: Öğrencinin dersi geçip geçmediğini gösterir (Evet/Hayır).
Bu veri setinde, “Dersi Geçti mi?” bizim hedef değişkenimizdir, yani tahmin etmeye çalıştığımız değişken budur. “Öğrenci” ve “Çalıştı mı?” sütunları ise özelliklerimizdir, yani hedef değişkeni tahmin etmek için kullanacağımız değişkenlerdir.
Bu örnek veri seti küçük ve basitleştirilmiş olsa da, karar ağacı oluşturma sürecini ve temel prensiplerini anlamak için iyi bir başlangıç noktası sunmaktadır. Daha sonraki bölümlerde, bu veri setini kullanarak bir karar ağacı oluşturacak ve öğrenci başarısını tahmin etme yeteneğini değerlendireceğiz.
3. Entropi ve Bilgi Kazancı
Karar ağaçları, verileri en iyi şekilde bölmek için en bilgilendirici özellikleri seçerek çalışır. Bu, entropi ve bilgi kazancı gibi kavramları kullanarak başarılır.
Entropi, bir veri setindeki belirsizliğin veya rastgeleliğin bir ölçüsüdür. Örneğin, bir sınıftaki tüm öğrenciler aynı dersi geçtiyse, entropi sıfırdır, çünkü sonuçta hiçbir belirsizlik yoktur. Ancak, öğrencilerin yarısı dersi geçip yarısı kalırsa, entropi yüksek olur, çünkü sonuç daha belirsizdir.
Entropi matematiksel olarak şu şekilde ifade edilir:
Entropi(S) = - Σ p(x) * log2(p(x))
Burada:
- S: Veri seti
- p(x): Her bir sınıfın olasılığı
Bilgi kazancı, bir özelliğe göre verileri böldüğümüzde entropideki azalmayı temsil eder. Amaç, bilgi kazancını en üst düzeye çıkaran özelliği seçmektir. Bir özelliğin bilgi kazancı ne kadar yüksekse, verileri sınıflandırmada o kadar etkili olur.
Bilgi kazancı şu şekilde hesaplanır:
Bilgi Kazancı(S, A) = Entropi(S) - Σ (|Sv| / |S|) * Entropi(Sv)
Burada:
- S: Orijinal veri seti
- A: Bölmek için kullanılan özellik
- Sv: A özelliğinin belirli bir değeri için oluşturulan alt küme
- |S|: S veri setindeki örnek sayısı
- |Sv|: Sv alt kümesindeki örnek sayısı
Bu formüllere göre ilgili hesaplamaları yaptığımızda erişilen sonuçlar aşağıdaki gibidir:
1. Hedef Değişkenin Entropisi:
- Toplam 6 öğrencimiz var.
- 4 öğrenci dersi geçti (Evet), 2 öğrenci dersi geçemedi (Hayır).
- P(Evet) = 4/6 = 2/3
- P(Hayır) = 2/6 = 1/3
- Entropi(Dersi Geçti mi?) = — P(Evet) * log2(P(Evet)) — P(Hayır) * log2(P(Hayır))
- Entropi(Dersi Geçti mi?) = — (2/3) * log2(2/3) — (1/3) * log2(1/3)
- Entropi(Dersi Geçti mi?) ≈ 0.918
2. “Çalıştı mı?” Özelliğine Göre Entropi:
“Evet” için:
- 3 öğrenci çalıştı ve dersi geçti.
- Entropi(Evet) = — (3/3) * log2(3/3) = 0 (Tamamen homojen, bu yüzden entropi 0)
“Hayır” için:
- 1 öğrenci çalışmadı ve dersi geçti.
- 2 öğrenci çalışmadı ve dersi geçemedi.
- P(Evet) = 1/3
- P(Hayır) = 2/3
- Entropi(Hayır) = — (1/3) * log2(1/3) — (2/3) * log2(2/3) ≈ 0.918
3. “Çalıştı mı?” Özelliğinin Bilgi Kazanımı:
- Bilgi Kazanımı = Entropi(Hedef Değişken) — ∑ [P(Özellik Değeri) * Entropi(Özellik Değeri)]
- Bilgi Kazanımı(“Çalıştı mı?”) = 0.918 — [(3/6)*0 + (3/6)*0.918]
- Bilgi Kazanımı(“Çalıştı mı?”) ≈ 0.459
4. “Öğrenci” Özelliğine Göre Entropi:
- Sibel için:
- 1 kez geçti, 1 kez kaldı.
- P(Evet) = 1/2
- P(Hayır) = 1/2
- Entropi(Sibel) = — (1/2) * log2(1/2) — (1/2) * log2(1/2) = 1
- Mehmet için:
- 1 kez geçti, 1 kez kaldı.
- P(Evet) = 1/2
- P(Hayır) = 1/2
- Entropi(Mehmet) = — (1/2) * log2(1/2) — (1/2) * log2(1/2) = 1
- İpek için:
- 2 kez geçti, 0 kez kaldı.
- P(Evet) = 2/2 = 1
- P(Hayır) = 0/2 = 0
- Entropi(İpek) = — (1) * log2(1) — (0) * log2(0) = 0 (log2(0) tanımsız olduğu için 0 olarak kabul edilir)
5. “Öğrenci” Özelliğinin Bilgi Kazanımı:
- Bilgi Kazanımı = Entropi(Hedef Değişken) — ∑ [P(Özellik Değeri) * Entropi(Özellik Değeri)]
- Bilgi Kazanımı(“Öğrenci”) = 0.918 — [(2/6) * 1 + (2/6) * 1 + (2/6) * 0]
- Bilgi Kazanımı(“Öğrenci”) = 0.918–2/3
- Bilgi Kazanımı(“Öğrenci”) ≈ 0.251
Sonuç:
- “Öğrenci” özelliğinin bilgi kazanımı 0.251’dir.
- Bu, “Öğrenci” bilgisinin hedef değişkeni (“Dersi Geçti mi?”) belirlemede “Çalıştı mı?” özelliğinden (bilgi kazanımı: 0.459) daha az etkili olduğunu gösterir.
Yani, “Öğrenci” özelliği de bir miktar bilgi sağlıyor, ancak “Çalıştı mı?” özelliği kadar etkili değil. Bu nedenle karar ağacı oluşturulurken ilk olarak “Çalıştı mı?” özelliği kullanılıyor.
Çalıştı mı?
/
Evet Hayır
/
Evet Öğrenci
/ |
Sibel Mehmet İpek
/ |
Hayır Hayır Evet
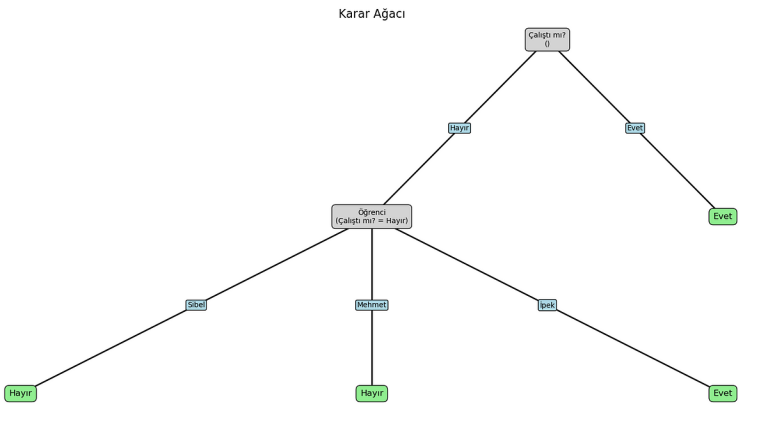
Kök düğüme “Çalıştı mı ?” değişkenini ekledikten sonra eğer “Çalıştı mı?” değişkeni “Evet” ise “Geçti mi?” hedef değişkeninin de evet olduğunu fark ettik. Devamında eğer “Çalıştı mı?” değişkeni “Hayır” ise bilgi kazancı 2. en yüksek olan diğer değişkene yani “Öğrenci” değişkenine bakmamız gerekiyordu. Yine tablomuzu incelersek Öğrenci de 3 değişken olduğundan bizim 3 durum üzerinden incelememiz gerekiyor ve tablo da Sibel ve Mehmet adlı öğrencilerin eğer “Çalıştı mı?” değişkeni “Hayır” değerini aldığında “Geçti mi?” hedef değişkeninin de “Hayır” değerini aldığını gözlemledik. Bu iki öğrencinin aksine İpek adlı öğrenci ise “Çalıştı mı?” değişkeni “Hayır” değerini almasına rağmen “Geçti mi?” hedef değişkeni “Evet” değerini alıyordu. Bunları da göz önünde bulundurduktan sonra sonuç olarak yukarıdaki gibi bir karar ağacı oluşturulabileceğine kanaat getirdik.
4.Python’da Karar Ağacı Oluşturma
Bu bölümde, verilen Python kodunu kullanarak karar ağacının nasıl oluşturulduğunu ve görselleştirildiğini adım adım açıklayacağız.
- Kütüphanelerin İçe Aktarılması:
import math
import pandas as pd
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
- math: Matematiksel işlemler için kullanılır (log2 fonksiyonu entropi hesaplamasında)
- pandas: Veri işleme için kullanılır (DataFrame oluşturma ve manipülasyonu)
- sklearn.tree: Karar ağacı algoritmasını içerir (plot_tree fonksiyonu ağacı görselleştirmek için)
- matplotlib.pyplot: Grafik çizimleri için kullanılır (ağacı görselleştirme)
2. Veri Setinin Oluşturulması:
information = {'Öğrenci': ['Sibel', 'Sibel', 'Mehmet', 'Mehmet', 'İpek', 'İpek'],
'Çalıştı mı?': ['Hayır', 'Evet', 'Hayır', 'Evet', 'Hayır', 'Evet'],
'Dersi Geçti mi?': ['Hayır', 'Evet', 'Hayır', 'Evet', 'Evet', 'Evet']}
df = pd.DataFrame(information)- Knowledge sözlüğü, öğrenci adı, çalışma durumu ve ders geçme durumunu içeren örnek veri setini tanımlar.
- pd.DataFrame(information) ile veri seti bir pandas DataFrame’ine dönüştürülür. DataFrame, veri manipülasyonu ve analizi için kullanışlı bir yapıdır.
3. Entropi Hesaplama Fonksiyonu:
def entropi(hedef_değişken):
değerler = hedef_değişken.value_counts()
toplam = len(hedef_değişken)
entropi = 0
for depend in değerler:
olasılık = depend / toplam
entropi -= olasılık * math.log2(olasılık)
return entropi
- Bu fonksiyon, verilen bir hedef değişken (sütun) için entropi değerini hesaplar. Entropi, veri setindeki belirsizliği veya rastgeleliği ölçer. Düşük entropi, veri setinin daha homojen olduğunu (aynı sınıfa ait örneklerin çoğunlukta olduğunu), yüksek entropi ise veri setinin daha heterojen olduğunu (farklı sınıflara ait örneklerin daha dengeli dağıldığını) gösterir.
- Fonksiyon, önce hedef değişken içindeki her bir sınıfın (değerler) kaç kez tekrar ettiğini sayar (value_counts()).
- Daha sonra, her sınıfın olasılığını (olasılık) hesaplar ve bu olasılıkları entropi formülünde kullanarak toplam entropiyi hesaplar.
4. Bilgi Kazancı Hesaplama Fonksiyonu:
def bilgi_kazanci(veri, özellik, hedef_değişken):
toplam_entropi = entropi(veri[hedef_değişken])
özellik_değerleri = veri[özellik].distinctive()
ağırlıklı_entropi = 0
for değer in özellik_değerleri:
altküme = veri[veri[özellik] == değer]
altküme_entropi = entropi(altküme[hedef_değişken])
ağırlıklı_entropi += (len(altküme) / len(veri)) * altküme_entropi
return toplam_entropi - ağırlıklı_entropi
- Bu fonksiyon, belirli bir özellik (sütun) kullanılarak veri setinin bölünmesinin sağlayacağı bilgi kazancını hesaplar. Bilgi kazancı, bölünme sonucunda entropinin ne kadar azaldığını gösterir. Daha yüksek bilgi kazancı, daha etkili bir bölünme anlamına gelir.
- Fonksiyon, önce hedef değişken için toplam entropiyi hesaplar.
- Ardından, belirli özelliğin her bir benzersiz değeri için alt kümeler oluşturur ve bu alt kümelerin entropilerini hesaplar.
- Alt kümelerin entropileri, veri setindeki oranlarıyla ağırlıklandırılarak toplanır (ağırlıklı_entropi) ve toplam entropiden çıkarılarak bilgi kazancı bulunur.
5. Karar ağacı sınıfı
class KararAgaci:
def __init__(self, veri, hedef_değişken):
self.veri = veri
self.hedef_değişken = hedef_değişken
self.kök = self.düğüm_oluştur(veri)def düğüm_oluştur(self, veri):
özellikler = veri.columns.drop(self.hedef_değişken)
# Eğer özellik kalmadıysa veya hedef değişken tek bir değere sahipse, yaprak düğüm oluştur
if len(özellikler) == 0 or len(veri[self.hedef_değişken].distinctive()) == 1:
return veri[self.hedef_değişken].mode()[0]
# Bilgi kazancı en yüksek olan özelliği bul
en_iyi_özellik = max(özellikler, key=lambda özellik: bilgi_kazanci(veri, özellik, self.hedef_değişken))
# Düğümü oluştur ve en iyi özelliği ata
düğüm = {'özellik': en_iyi_özellik, 'çocuklar': {}}
# En iyi özelliğin her bir değeri için alt küme oluştur ve alt düğümler oluştur
for değer in veri[en_iyi_özellik].distinctive():
altküme = veri[veri[en_iyi_özellik] == değer]
düğüm['çocuklar'][değer] = self.düğüm_oluştur(altküme)
return düğüm
- Bu sınıf, karar ağacını oluşturmak ve kullanmak için gerekli fonksiyonları içerir.
- __init__ fonksiyonu, sınıfın başlatıcı fonksiyonudur. Veri setini ve hedef değişken sütun adını alır. Ağacın kök düğümünü (self.kök) düğüm_oluştur fonksiyonunu çağırarak oluşturur.
- düğüm_oluştur fonksiyonu, verilen veri seti için en iyi bölünmeyi bulur ve alt düğümleri özyinelemeli olarak oluşturur. Bu fonksiyon, önce bölünecek özellik kalıp kalmadığını veya hedef değişkenin tek bir değere sahip olup olmadığını kontrol eder. Eğer bu koşullar sağlanıyorsa, yaprak düğüm oluşturulur ve bu düğüm hedef değişkenin en sık görünen sınıfını temsil eder. Aksi takdirde, fonksiyon bilgi kazancını maksimize eden özelliği bulur (en_iyi_özellik) ve bu özellik kullanılarak alt düğümler oluşturulur. Bu işlem özyinelemeli olarak devam eder.
- tahmin_et fonksiyonu, verilen bir örnek için ağacı kullanarak tahmin yapar. Örnek, ağacın kök düğümünden başlayarak, her düğümde özelliğin değerine göre alt düğümlere yönlendirilir. Sonunda yaprak düğüme ulaşıldığında, bu düğümün temsil ettiği sınıf, örnek için tahmin edilen sınıf olur.
6. Ağacı Çizdirme Fonksiyonu
def ağacı_çizdir(düğüm, x=0, y=0, yatay_aralık=1, dikey_aralık=1, koşul=""):
if isinstance(düğüm, dict):
plt.textual content(x, y, f"{düğüm['özellik']}n({koşul})", ha='heart', va='heart',
bbox=dict(facecolor='lightgray', edgecolor='black', boxstyle='spherical,pad=0.5'))
for i, (değer, çocuk) in enumerate(düğüm['çocuklar'].objects()):
yeni_x = x + (i - len(düğüm['çocuklar'])/2 + 0.5) * yatay_aralık
# Dallanma koşulunu dal üzerine yazdır
plt.textual content((x + yeni_x) / 2, (y + y - dikey_aralık) / 2, f"{değer}", ha='heart', va='heart',
bbox=dict(facecolor='lightblue', edgecolor='black', boxstyle='spherical,pad=0.2'))
plt.plot([x, yeni_x], [y, y - dikey_aralık], 'k-', linewidth=2)
# Dallanma koşullarını ekleme
if koşul:
yeni_koşul = f"{koşul} ve {düğüm['özellik']} = {değer}"
else:
yeni_koşul = f"{düğüm['özellik']} = {değer}"
ağacı_çizdir(çocuk, yeni_x, y - dikey_aralık, yatay_aralık, dikey_aralık, koşul=yeni_koşul)
else:
plt.textual content(x, y, düğüm, ha='heart', va='heart', fontsize=12,
bbox=dict(facecolor='lightgreen', edgecolor='black', boxstyle='spherical,pad=0.5'))
- Bu fonksiyon, oluşturulan karar ağacını matplotlib kütüphanesi kullanılarak görselleştirir. Düğümleri, dalları ve yaprakları ekrana çizer. Fonksiyon, ağacın yapısını özyinelemeli olarak dolaşarak, her düğüm için koordinatlar hesaplar ve düğümün özellik adını ve dallanma koşullarını metin olarak ekler.
7.Karar Ağacı Oluşturma ve Görselleştirme
ağaç = KararAgaci(df, 'Dersi Geçti mi?')plt.determine(figsize=(12, 10)) # Figür boyutunu büyütme
ağacı_çizdir(ağaç.kök, yatay_aralık=3, dikey_aralık=1.5)
plt.axis('off')
plt.title("Karar Ağacı", fontsize=16) # Başlık ekleme
plt.present()
- Karar Ağacı Oluşturma ve Görselleştirme:
- ağaç = KararAgaci(df, ‘Dersi Geçti mi?’) ile KararAgaci sınıfından bir örnek oluşturulur ve veri seti ve hedef değişken sütun adı belirtilir.
- plt.determine(figsize=(12, 10)) ile çizim alanı boyutu belirlenir.
- ağacı_çizdir(ağaç.kök, yatay_aralık=3, dikey_aralık=1.5) ile ağaç görselleştirilir.
- plt.axis(‘off’) ile eksenler kapatılır.
- plt.title(“Karar Ağacı”, fontsize=16) ile çizime başlık eklenir.
- plt.present() ile çizim ekranda gösterilir.
- Alınan çıktı da aşağıdaki gibidir:
5.Karar Ağaçlarının Avantajları ve Sınırlamaları
Karar ağaçları, makine öğrenmesinde yaygın olarak kullanılan güçlü ve popüler algoritmalardır. Bununla birlikte, her algoritma gibi, karar ağaçlarının da kendine özgü avantajları ve sınırlamaları vardır.
Avantajları:
- Anlaşılabilirlik: Ağacın yapısı, verilerin nasıl sınıflandırıldığına dair internet bir resim sunar. Bu, özellikle modelin karar verme sürecini anlamanın önemli olduğu durumlarda faydalıdır.
- Veri ön işleme ihtiyacının az olması: Karar ağaçları, verilerin ön işleme konusunda diğer algoritmalar kadar talepkar değildir. Örneğin, verileri ölçeklendirmek veya merkezlemek genellikle gerekli değildir.
- Hem sayısal hem de kategorik verileri işleyebilme: Karar ağaçları, hem sayısal hem de kategorik verileri işleyebilir. Bu, onları çeşitli veri türlerine sahip problemler için uygun hale getirir.
- Göreceli olarak hızlı eğitim süresi: Karar ağaçları, özellikle diğer karmaşık algoritmalara kıyasla nispeten hızlı bir şekilde eğitilebilir.
Sınırlamaları:
- Aşırı uyum: Karar ağaçları, eğitim verilerine aşırı uyum sağlamaya eğilimlidir. Bu, modelin eğitim verilerindeki örüntüleri çok iyi öğrendiği, ancak yeni, görünmeyen verilere genelleyemediği anlamına gelir. Aşırı uyumu önlemek için budama gibi teknikler kullanılır.
- Dengesiz veri setlerinde kötü performans: Karar ağaçları, sınıflarda dengesizlik olan veri setlerinde iyi performans göstermeyebilir. Bu durumda, mannequin, çoğunluk sınıfını doğru bir şekilde tahmin etmeye odaklanabilir ve azınlık sınıfını göz ardı edebilir.
- Veri hassasiyeti: Karar ağaçları, eğitim verilerindeki küçük değişikliklere karşı hassas olabilir. Bu, veri setindeki küçük bir değişikliğin, ağacın yapısını ve sonuç olarak modelin tahminlerini önemli ölçüde değiştirebileceği anlamına gelir.
Sonuç olarak, karar ağaçları, anlaşılırlık ve kullanım kolaylığı gibi önemli avantajlar sunan güçlü bir makine öğrenmesi algoritmasıdır. Ancak, aşırı uyum ve veri hassasiyeti gibi sınırlamaları da göz önünde bulundurmak önemlidir. Bu sınırlamaları azaltmak için budama, sınıflara ağırlık atama ve topluluk öğrenme yöntemleri gibi çeşitli teknikler kullanılabilir.
6.Sonuç
Bu çalışma, karar ağaçlarının temel prensiplerini ve öğrenci başarısını tahmin etme gibi basit bir senaryoda nasıl uygulanabileceğini göstermiştir. Entropi ve bilgi kazancı kavramları, veri setini en etkili şekilde bölmek ve bilgilendirici özellikleri seçmek için nasıl kullanılabileceğini gördük.
Python’daki basit bir karar ağacı uygulaması ile, “Çalıştı mı?” özelliğinin, öğrencilerin dersi geçip geçmeyeceğini tahmin etmede önemli bir faktör olduğunu gözlemledik. Elbette, gerçek dünya senaryolarında öğrenci başarısı çok daha karmaşık faktörlere bağlıdır ve daha kapsamlı veri setleri ve daha sofistike modeller gerektirdiğini de unutmayalım.
Bu çalışmada ele alınan temel prensipler ve uygulama örnekleri, karar ağaçlarının potansiyelini ve çok çeşitli problemleri çözmek için nasıl kullanılabileceğini göstermektedir. Karar ağaçları, veri bilimi alanında önemli bir araç olmaya devam etmekte ve gelecekte daha da yenilikçi uygulamaların ortaya çıkması beklenmektedir.