The formulation of the Spearman coefficient is analogous to Pearson’s coefficient, however it makes use of the ranks of the values in every variable as a substitute of the values themselves. It’s often given the Greek letter (theta). I’ll use the letter s to write down it in Latin characters. The next formulation provides the equation of the Spearman correlation coefficient s:
Once we evaluate this formulation with Pearson’s correlation coefficient r, we uncover that it solely replaces the values of x and y by their ranks U and V. One may say that the Spearman coefficient is Pearson’s coefficient utilizing the ranks! That’s why it’s referred to as the Spearman’s rank-correlation coefficient. Additionally, as a result of it’s computed utilizing the ranks and never the values, it is usually categorised as nonparametric.
Just like the case of Pearson’s coefficient, the p-value is calculated from t-distribution with the t-value given by the next formulation:
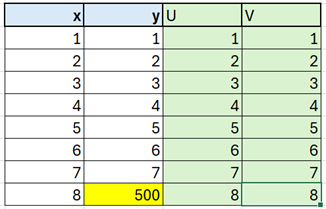
Desk 3 reveals the ranks U and V of the variables x and y in Desk 2.
On this case, the Spearman coefficient can be precisely 1, indicating a 100% correlation between the variables x and y ranks.
Now comes the query: when will we use ranks (Spearman), and when will we use the values (Pearson)? We are able to summarize the reply within the following two conditions:
(1) Once we count on that the values of the 2 variables in query don’t have outliers or important errors, we must always choose the Pearson’s coefficient.
(2) We use the Spearman coefficient once we don’t care concerning the values and solely must know the path of the connection between the 2 variables and when there’s a excessive probability of outliers and errors.
The Pearson’s coefficient is often a good selection for measurements originating from bodily methods and variables the place the values matter. Then again, knowledge from social research originating from questionnaires, for instance, once we ask respondents to offer ranked solutions, are good candidates for the Spearman’s coefficient.