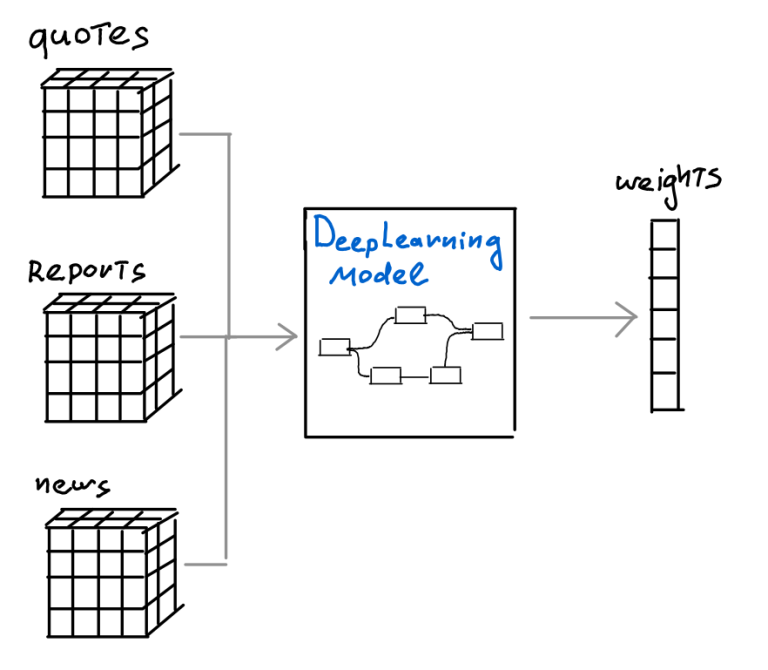
The total code for this situation is on the market at this hyperlink: https://github.com/survexman/deep_learning_portfolio_optimization/blob/master/scenario/synthetic_variational_allocation.py
Let’s study the applying of the mannequin we constructed on artificial returns knowledge.
Preliminary values are set for the random quantity mills within the numpy and PyTorch libraries to make sure the reproducibility of the outcomes:
seed = 5# numpy==1.24.1
import numpy as np
# torch==2.1.0
import torch
torch.manual_seed(seed)
np.random.seed(seed)
Variables for time collection, belongings, and rolling window parameters. Knowledge indices are separated into coaching and take a look at units:
n_timesteps, n_assets = 2000, 5
lookback, hole, horizon = 40, 2, 10n_samples = n_timesteps - lookback - horizon - hole + 1
split_ix = int(n_samples * 0.8)
indices_train = record(vary(split_ix))
indices_test = record(vary(split_ix + lookback + horizon, n_samples))
Producing artificial sinusoidal time collection for asset returns with random noise. Imply returns are calculated, and a graph is plotted:
# Artificial sinusoidal returns
from utils.data_utils import sin_singlereturns = np.array(
[
sin_single(
n_timesteps,
freq = 1 / np.random.randint(3, lookback),
amplitude = 0.01,
phase = np.random.randint(0, lookback)
) for _ in range(n_assets)
]
).T
# We additionally add some noise.
returns += np.random.regular(scale = 0.002, dimension = returns.form)
# Imply returns
print(f'Imply returns: {spherical(sum(np.imply(returns, axis = 0)), 5)}')
# Imply returns: 0.00013
# Plot returns
# matplotlib==3.7.2
import matplotlib.pyplot as plt
plt.title('Returns')
plt.plot(returns[:100, 0:(n_assets - 1)])
plt.present()
The typical return of all belongings is near zero: 0.00013
Subsequent, we create a rolling window to type the enter knowledge (X) and goal variables (y) for coaching the mannequin. This knowledge processing method prepares the time collection for mannequin coaching:
# Creating sliding window units
X_list, y_list = [], []for i in vary(lookback, n_timesteps - horizon - hole + 1):
X_list.append(returns[i - lookback: i, :])
y_list.append(returns[i + gap: i + gap + horizon, :])
X = np.stack(X_list, axis = 0)[:, None, ...]
y = np.stack(y_list, axis = 0)[:, None, ...]
print(f'X: {X.form}, y: {y.form}')
We create coaching and testing datasets utilizing the instruments of the Deepdow library:
# deepdow==0.2.2
from deepdow.knowledge import InRAMDataset, RigidDataLoader, prepare_standard_scaler, Scalemeans, stds = prepare_standard_scaler(X, indices = indices_train)
dataset = InRAMDataset(X, y, remodel = Scale(means, stds))
batch_size = 512
dataloader_train = RigidDataLoader(
dataset,
indices = indices_train,
batch_size = batch_size
)
dataloader_test = RigidDataLoader(
dataset,
indices = indices_test,
batch_size = batch_size
)
A FullyConnectedTrivialNet is created. This kinds the core of the mannequin that will probably be used to foretell asset weights within the portfolio:
from mannequin.fully_connected_trivial_net import FullyConnectedTrivialNetcommunity = FullyConnectedTrivialNet(n_assets, lookback)
community = community.prepare()
The Sharpe ratio is used because the loss perform. Subsequent steps contain classical coaching of the mannequin:
from deepdow.losses import SharpeRatio
from torch.optim import Adamloss = SharpeRatio()
optimizer = Adam(community.parameters(), amsgrad = True)
train_epochs = 10
print('Coaching...')
for epoch in vary(train_epochs):
error_list = []
for batch_idx, batch in enumerate(dataloader_train):
X_batch, y_batch, timestamps, asset_names = batch
X_batch = X_batch.float()
y_batch = y_batch.float()
weights = community(X_batch)
error = loss(weights, y_batch).imply()
error_list.append(error.merchandise())
optimizer.zero_grad()
error.backward()
optimizer.step()
print(f'Epoch {epoch} | Error: {spherical(np.imply(error_list), 5)}')
After coaching, the mannequin is examined on the take a look at set. A portfolio weight vector is constructed for every pattern from the take a look at set:
community = community.eval()# Weights for the take a look at set
weights_list = []
timestamps_list = []
for X_batch, _, timestamps, _ in dataloader_test:
X_batch = X_batch.float()
weights = community(X_batch).detach().numpy()
weights_list.append(weights)
timestamps_list.lengthen(timestamps)
weights = np.concatenate(weights_list, axis = 0)
asset_names = [dataloader_test.dataset.asset_names[asset_ix] for asset_ix in dataloader_test.asset_ixs]
# pandas==1.5.3
import pandas as pd
weights_df = pd.DataFrame(
weights,
index = timestamps_list,
columns = asset_names
)
weights_df.sort_index(inplace = True)
Subsequent, let’s construct on the outcomes of the mannequin on the take a look at set and examine it with the mannequin of uniform asset distribution. For our mannequin simulation, we are going to carry out portfolio rebalancing each horizon step:
# Multiply the returns by the weights to get the portfolio returns.
# returns_df - empty DataFrame for storing portfolio returns with identical index as weights_df
model_returns_df, uniform_returns_df = pd.DataFrame(), pd.DataFrame()
model_returns_df.index, uniform_returns_df.index = weights_df.index, weights_df.indexuniform_weights = np.ones(n_assets) / n_assets
for idx in vary(indices_test[0], indices_test[-1] - hole - horizon, horizon):
i_model_returns = (np.array(weights_df.loc[idx].tolist()) * returns[idx + gap: idx + gap + horizon]).sum(axis = 1)
i_uniform_returns = (uniform_weights * returns[idx + gap: idx + gap + horizon]).sum(axis = 1)
# Retailer the returns within the DataFrame to vary [idx + gap: idx + gap + horizon]
model_returns_df.loc[idx + gap: idx + gap + len(i_model_returns) - 1, 'return'] = i_model_returns
uniform_returns_df.loc[idx + gap: idx + gap + len(i_uniform_returns) - 1, 'return'] = i_uniform_returns
# Drop the NaN values from the DataFrame.
model_returns_df.dropna(inplace = True)
uniform_returns_df.dropna(inplace = True)
To research the outcomes, we use the QuantStats framework, which permits creating an HTML report with the mannequin’s efficiency outcomes:
import os
# QuantStats==0.0.62
import quantstats as qsmodel_balance_df = (model_returns_df['return'] + 1).cumprod()
uniform_balance_df = (uniform_returns_df['return'] + 1).cumprod()
# Including index to the balance_df as days from 2000-01-01
model_balance_df.index = pd.date_range(begin = '2000-01-01', intervals = len(model_balance_df))
uniform_balance_df.index = pd.date_range(begin = '2000-01-01', intervals = len(uniform_balance_df))
current_dir = os.path.dirname(os.path.abspath(__file__))
report_path = os.path.be part of(current_dir, '../output/synth_variational_allocation/')
qs.studies.html(
model_balance_df,
title = 'Mannequin Outcomes for Artificial Variational Allocation',
output = report_path + 'model_results.html'
)
qs.studies.html(
uniform_balance_df,
title = 'Uniform Outcomes for Artificial Variational Allocation',
output = report_path + 'uniform_results.html'
)
Right here is the report with our mannequin’s outcomes:
And that is the report with the outcomes of the uniform asset distribution mannequin:
It’s straightforward to see that our mannequin exhibits glorious portfolio administration outcomes on the take a look at set in comparison with the uniform distribution mannequin.
In fact, the artificial knowledge we generated have a comparatively easy nature and don’t mirror the complete complexity of real-time collection knowledge. Nevertheless, our objective right here was to exhibit the essential ideas of the deep studying mannequin and show the suitability of this strategy for fixing the portfolio optimization drawback.