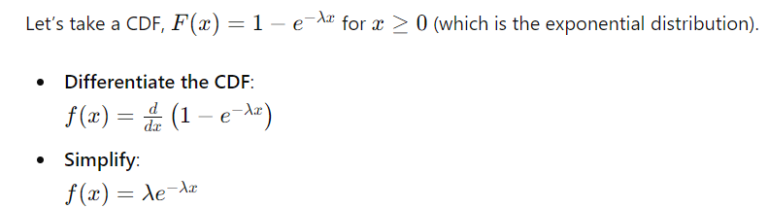After I first began exploring statistics, I keep in mind feeling overwhelmed by the sheer variety of phrases and equations. However as soon as I understood how PDF and CDF work collectively, every little thing began to click on. Right now, I wish to share that readability with you. Let’s demystify these ideas and see how they will remodel your understanding and utility of likelihood.
On this weblog submit, we’ll embark on an in depth journey by the world of PDFs and CDFs. First, I’ll information you thru the fundamentals of likelihood distributions, setting the stage for a deeper dive into our fundamental subjects. You’ll study what a Chance Density Perform is, the way it’s represented mathematically, and methods to visualize it. Then, we’ll discover the Cumulative Distribution Perform, breaking down its definition, properties, and sensible examples.
The guts of our dialogue would be the relationship between the PDF and CDF. I’ll present you methods to convert a PDF to a CDF by integration and methods to go the opposite method by differentiating a CDF to get the PDF. We’ll use loads of graphs and real-world examples for example these ideas, making them simpler to understand.
Fundamentals of Chance Distributions
Think about you’re rolling a good die. You recognize that every face (1 by 6) has an equal likelihood of touchdown face up. The idea that describes this chance for every consequence is named a likelihood distribution. In easy phrases, a likelihood distribution assigns possibilities to totally different outcomes of a random variable.
After I first encountered likelihood distributions, I used to be amazed at how they may very well be used to explain the chance of every little thing from cube rolls to the heights of individuals. Basically, a likelihood distribution is a mathematical operate that gives the chances of incidence of various attainable outcomes in an experiment.
Discrete vs. Steady Distributions:
Now, let’s break it down a bit extra. Chance distributions will be categorized into two fundamental varieties: discrete and steady.
- Discrete Distributions: These are used when the random variable can tackle a countable variety of distinct values. Consider issues just like the variety of college students in a classroom, the result of rolling a die, or the variety of automobiles passing by a toll sales space in an hour. Every of those eventualities has particular, separate values you may depend.
- Steady Distributions: These come into play when the random variable can tackle any worth inside a given vary. As an example, think about the precise peak of people, the time it takes to run a marathon, or the temperature on a specific day. These values aren’t countable as a result of they will embody decimals and fractions, making them steady.
After I began working with information, I discovered it essential to differentiate between these two varieties as a result of the strategies and instruments you utilize to investigate them differ considerably.
Understanding the Chance Density Perform (PDF)
The Chance Density Perform (PDF) is a basic idea in steady likelihood distributions. It’s a operate that describes the relative chance of a steady random variable taking up a particular worth. Not like discrete possibilities, which provide you with actual possibilities for every consequence, the PDF offers a density that have to be built-in over an interval to seek out possibilities.
In less complicated phrases, consider the PDF as a clean curve that reveals how the likelihood is distributed throughout totally different values. After I first understood this, it was like a lightweight bulb going off — realizing that the realm below this curve over an interval offers you the likelihood for that interval was a game-changer.
Mathematical Illustration:
Mathematically, for a steady random variable X with PDF f(x), the likelihood that X falls inside the interval [a,b] is given by the integral:
Listed below are some key properties of the PDF:
- Non-Unfavourable: The PDF is at all times non-negative, f(x)≥0, as a result of possibilities can’t be unfavorable.
- Whole Space Equals 1: The full space below the PDF curve is the same as 1, representing the truth that the likelihood of all attainable outcomes mixed is 1.
Understanding these properties helped me grasp how PDFs work and why they’re so helpful in modeling steady random variables.
Graphical Illustration:
Visualizing PDFs could make the idea a lot clearer. Listed below are a couple of examples of frequent PDFs:
- Regular Distribution: The basic bell curve, which is symmetric across the imply. It’s used to mannequin many pure phenomena like heights, take a look at scores, and measurement errors.
2. Exponential Distribution: Typically used to mannequin the time between occasions in a Poisson course of, such because the time between arrivals of buses at a bus cease.
After I began visualizing these distributions, it turned a lot simpler to grasp how totally different phenomena may very well be modeled and analyzed.
Sensible Examples:
Let’s deliver this to life with some sensible examples:
- Peak Distribution: Should you measure the heights of a giant group of individuals, you’ll seemingly discover that most individuals’s heights cluster round a median worth, with fewer individuals being extraordinarily quick or tall. This distribution of heights will be modeled by a traditional distribution.
- Weight Distribution: Equally, the weights of people in a inhabitants will be described utilizing a traditional distribution, the place most weights are across the common, with fewer individuals being extraordinarily gentle or heavy.
By occupied with these real-world examples, you can begin to see how PDFs present a robust method to describe and predict outcomes in numerous fields, from biology to finance.
Understanding the Cumulative Distribution Perform (CDF)
Definition of CDF:
Whenever you’re working with likelihood distributions, understanding the Cumulative Distribution Perform (CDF) is essential. The CDF offers you a complete method to describe the likelihood {that a} random variable will tackle a worth lower than or equal to a specific worth. Consider it as a working whole of possibilities, accumulating as you progress alongside the vary of attainable values.
In less complicated phrases, the CDF of a random variable X is a operate F(x) that gives the likelihood that X shall be lower than or equal to xxx. After I first realized about CDFs, I noticed how highly effective they’re in summarizing all the distribution of a variable, permitting us to see the likelihood build-up over a spread.
Mathematical Illustration:
Mathematically, the CDF is outlined as:
For a steady random variable with a PDF f(x)f(x)f(x), the CDF will be expressed because the integral of the PDF from −∞ to x:
Listed below are some essential properties of the CDF:
- Monotonic: The CDF is a non-decreasing operate, which means as xxx will increase, F(x) both stays the identical or will increase.
- Ranges from 0 to 1: The CDF begins at 0 when x is at its minimal worth and approaches 1 as x approaches its most worth. This aligns with the concept the whole likelihood for all attainable outcomes is 1.
These properties make the CDF an important device for understanding how possibilities accumulate and unfold over totally different values.
Graphical Illustration:
Visualizing CDFs can drastically improve your understanding. Listed below are a couple of examples of frequent CDFs:
- Regular Distribution CDF: This S-shaped curve reveals how possibilities accumulate for a usually distributed variable. The center a part of the curve is steeper, indicating that almost all values are near the imply.
2. Exponential Distribution CDF: This curve rises rapidly initially after which ranges off, reflecting the fast accumulation of likelihood in the beginning and slower accumulation as values improve.
Seeing these graphs, you may recognize how totally different distributions accumulate possibilities in distinctive methods.
Sensible Examples:
Let’s have a look at some real-world examples the place CDFs come into play:
- Revenue Distribution: Should you plot the CDF of earnings in a inhabitants, you may see what quantity of individuals earn under a specific amount. For instance, you may discover that fifty% of individuals earn lower than $50,000 per 12 months.
- Examination Scores: Suppose you might have the examination scores of a giant group of scholars. By plotting the CDF, you may decide the likelihood {that a} scholar scored under a sure threshold. As an example, you might discover the likelihood {that a} scholar scored lower than 80%.
Understanding these real-world functions helps you see the sensible worth of CDFs in analyzing and deciphering information.
Relationship Between PDF and CDF
Integral Relationship
Let’s dive into the connection between the Chance Density Perform (PDF) and the Cumulative Distribution Perform (CDF). One of many key relationships is that the CDF is the integral of the PDF. Think about you’re filling up a tank of water; the speed at which you pour water into the tank is analogous to the PDF, whereas the quantity of water within the tank at any level is just like the CDF.
Mathematically, this relationship is expressed as:
Right here, F(x) is the CDF, and f(t) is the PDF. What this implies is that to seek out the CDF at a specific worth x, you combine the PDF from −∞ as much as x.
Differentiation Relationship
On the flip aspect, when you’ve got the CDF and it’s essential to get again to the PDF, you are able to do this by differentiation. Consider the CDF as the whole quantity of water within the tank at any given time. If you wish to learn how quick the water is being poured in at any second, you are taking the by-product of the CDF.
Mathematically, it seems like this:
So, the PDF is just the by-product of the CDF with respect to xxx.
Graphical Illustration
Now, let’s visualize this relationship. Image a bell curve representing a traditional distribution. The bell curve is your PDF. Beneath it, you might have an S-shaped curve rising from left to proper — that is your CDF. The steepest a part of the S-curve corresponds to the height of the bell curve. This visible can assist you perceive how the realm below the PDF provides as much as kind the CDF.
Changing PDF to CDF
Step-by-Step Course of
Whenever you wish to convert a PDF to a CDF, you’re primarily integrating the PDF. Right here’s an easy course of:
- Determine the PDF: Let’s say you might have f(x).
- Set Up the Integral: You’ll combine f(x) from −∞ to xxx.
- Carry out the Integration: Calculate:
- Consider: The result’s your CDF, F(x).
Examples and Workouts
For apply, let’s think about a easy PDF
Changing CDF to PDF
Step-by-Step Course of
In case you have a CDF and it’s essential to discover the PDF, differentiation is your device. Right here’s the method:
- Determine the CDF: Let’s say you might have F(x).
- Differentiate: Calculate the by-product of F(x)F(x)F(x) with respect to x.
- Consider: The result’s your PDF, f(x).
Examples and Workouts
Strive these steps with totally different capabilities to get snug with the method. Should you want extra apply, let’s arrange a couple of workouts with detailed options to solidify your understanding.
Functions in Information Science and Statistics
PDFs and CDFs are basic in information science and statistics. Their functions span numerous fields, from threat evaluation to machine studying fashions. Let’s break it down:
- Danger Evaluation: In finance, PDFs are used to mannequin the chance of various outcomes. For instance, the PDF of inventory returns can assist you perceive the likelihood of maximum losses or positive aspects. The CDF helps in calculating Worth at Danger (VaR), a measure used to evaluate the danger of an funding.
- Machine Studying Fashions: Many machine studying algorithms, resembling Naive Bayes classifiers and Gaussian Combination Fashions (GMM), depend on PDFs. As an example, Naive Bayes makes use of PDFs to calculate the chance of information factors belonging to totally different lessons. In GMM, the info is modeled as a mix of a number of Gaussian distributions, every represented by its personal PDF.
- Speculation Testing: In statistics, PDFs are essential for understanding distributions below totally different hypotheses. Whenever you carry out a t-test, chi-square take a look at, or some other statistical take a look at, you’re working with PDFs to find out p-values, which inform you the likelihood of observing your information below the null speculation.
- Reliability Engineering: PDFs and CDFs are used to mannequin the time till failure of parts in reliability engineering. For instance, the Weibull distribution, which is used to mannequin life information, will be analyzed by its PDF to seek out the failure charge and thru its CDF to find out the likelihood of failure by a sure time.
Case Research
To make this extra tangible, let’s have a look at some sensible examples the place PDFs and CDFs play a vital function:
- Predicting Buyer Churn: A telecommunications firm needs to foretell buyer churn. By analyzing historic information, they will mannequin the time till churn (buyer leaving) utilizing a survival evaluation strategy. The PDF offers the speed at which clients are anticipated to churn at totally different instances, whereas the CDF offers the likelihood {that a} buyer can have churned by a sure time. This info helps in designing retention methods.
- Credit score Scoring: Banks use PDFs to mannequin the distribution of credit score scores amongst their clients. By analyzing this distribution, they will decide the chance of default for various credit score rating ranges. The CDF helps in setting thresholds for mortgage approvals by offering the cumulative likelihood of default as much as a sure rating.
- Medical Analysis: In medical trials, researchers use PDFs and CDFs to investigate the time till an occasion happens, resembling restoration or loss of life. For instance, in most cancers analysis, the PDF may present the speed at which sufferers are anticipated to relapse over time, whereas the CDF offers the likelihood of relapse inside a given interval. This helps in evaluating the effectiveness of therapies.
Last Ideas
Understanding PDFs and CDFs is essential for anybody concerned in information science and statistics. These capabilities are the spine of likelihood idea and statistical evaluation, offering a framework for making knowledgeable selections primarily based on information. Whether or not you’re assessing threat, constructing predictive fashions, or conducting speculation assessments, PDFs and CDFs are instruments that you just’ll depend on repeatedly.
In apply, mastering these ideas can considerably improve your skill to interpret and manipulate information. As you delve deeper into information science, you’ll discover {that a} strong grasp of PDFs and CDFs opens up new prospects for evaluation and perception. So, take the time to grasp these foundations — they’re important on your journey in information science and statistics.