Վիճակագրական տվյալները բաժանվում են 3 հիմնական խմբի․
1․ թվային (numerical)
2. կատեգորիկ (categorical)
3. հերթական (ordinal)
1. Թվային տվյալները ներառում են ինչպես դիսկրետ (դասարանում սովորողների քանակ), այնպես էլ անընդհատ արժեքներ (մարդու հասակ)։
2. Կատեգորիկ տվյալները բաժանվում են առանձին խմբերի։ Օրինակ՝ գույներ, մեքենաների տեսակներ։ Կատեգորիկ տվյալները թվայինի վերածելիս չեն կարող հերթականորեն համարակալվել։ Օրինակ՝ ունենք 3 գույն՝ դեղին, կարմիր, կանաչ։ Չենք կարող դեղին գույնին վերագրել 0, կարմիրին՝ 1, կանաչին՝ 2, քանի որ նրանց մեջ ոչ մի հերթականություն չկա և մոդելը ուսուցանելիս այն կարող է մտածել, որ կանաչ գույնը ավելի մեծ կարևորություն է ցույց տալիս քան դեղինը։ Այդ պատճառով օգտագործվում են one-hot վեկտորները։ 3 կատեգորիայի դեպքում մենք կունենանք 3 վեկտոր.
Տվյալների one-hot վեկտորների փոխակերպելու գործընթացը կոչվում է one-hot encoding:
3. Հերթական տվյալները նման են կատեգորիկ տվյալներին, բայց ի տարբերություն կատեգորիկի կարող ենք համարակալել, քանի որ նրանք ցույց են տալիս ինչ որ հերթականություն։ Օրինակ՝ վաճառողուհու սպասարկումը կարող ենք գնահատել 3 տարբերակով՝ “վատ”, “միջին”, “լավ”։ Հետևյալ 3 կատեգորիա-ները կարող ենք փոխարինել համապատասխանաբար 0, 1, 2 թվերով, քանի որ “լավ” գնահատականը ավելի մեծ է, քան “վատ” գնահատականը։
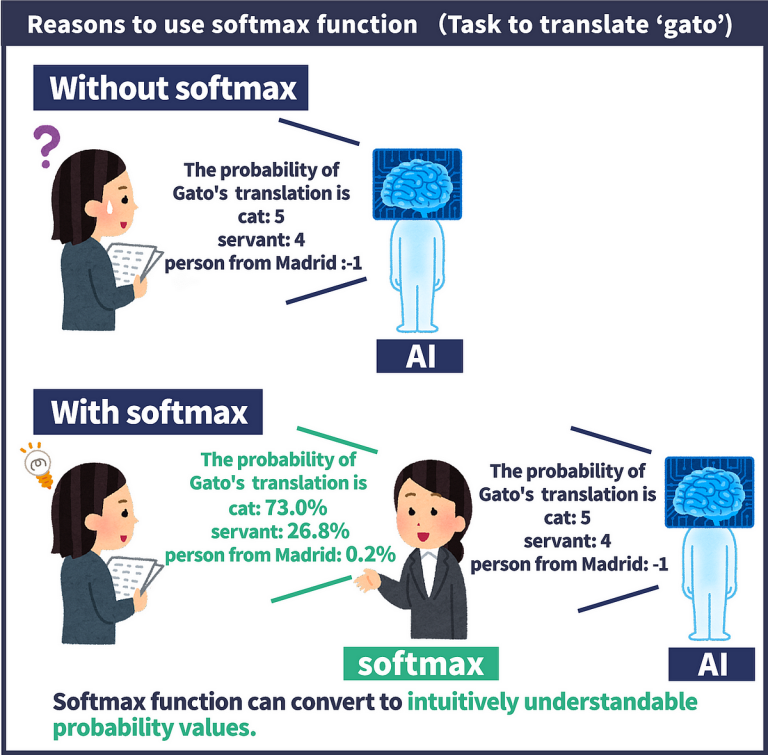
Ներմուծենք հավանականային վեկտոր գաղափարը։ Վեկտորը կոչվում է հավանականային, եթե նրա բոլոր կոորդինատները մեծ են 0-ից և կոորդինատների գումարը հավասար է մեկի։
Ունենք (xᵢ , yᵢ ), xᵢ ∈ Rᵏ, yᵢ ∈ Rᵐ տվյալների զույգեր։ yᵢ-ն ներկայաց-նում է one-hot վեկտոր։ Սահմանենք ֆունկցիա, որը մեզ կվերադարձնի հավանականային վեկտոր։
Մեր նպատակն է գտնել այնպիսի (bᵢ , wᵢ) պարամետրեր, որ f(xᵢ) ≈ yᵢ , i = 1, . . . n և ոչ միայն մեր ունեցած տվյալների համար։ Օրինակ՝ xᵢ ∼ նկար, yᵢ ∼ պիտակ (շուն, կատու, փիղ)։ Հետևյալ խնդիրը լուծելու համար օգտագործենք cross-entropy կորստի ֆունկցիան մի քանի պիտակի դեպքում։
Երկու պիտակի դեպքում այն ուներ հետևյալ տեսքը․
Մի քանի պիտակի դեպքում այն ունի հետևյալ տեսքը.
yᵢ ∈ one-hot վեկտոր, f(xᵢ) ∈ հավանականային վեկտոր, m-ը՝ պիտակների քանակ։ yᵢᵏ -ն ընդունում է 1 կամ 0 արժեք (one-hot վեկտոր): 1 արժեք ընդունելու դեպքում մեզ պետք է մինիմիզաց-նել “−ln(f(xᵢ)ᵏ )”, որը իր փոքրագույն արժեքը ընդունում է, երբ
f(xᵢᵏ) = 1 (հավանականային վեկտոր): Օրինակ՝ երբ մեր նկարի պիտակը եղել է շուն և մոդելը 100% վստահությամբ ասել
է շուն, այդ դեպքում մեր կորուստը կլինի 0։ Նկատենք որ (1) կորստի ֆունկցիան նույնն է, ինչ (2) կորստի ֆունկցիան, երբ պիտակների քանակը հավասար է 2։
Այս երկու պայմանը հաշվի առնելով և տեղադրելով (2) կորստի ֆունկցիայի մեջ, կստանանք (1) կորստի ֆունկցիան։
Իսկ ինչպե՞ս կարող ենք սոֆթմաքս դասակարգիչը ներկայաց-նել, որպես նեյրոնային ցանց։ f(x) ֆունկցիային նայելիս կարող ենք տեսնել, որ այն իրենից ներկայացնում է m հատ գծային
ֆունկցիա։ Այսինքն կունենանք m հատ նեյրոնից բաղկացած նեյրոնային ցանց և ակտիվացիոն ֆունկցիան սոֆթմաքս։