Hello All,
On this article, I’ll break down Varclus(Variable Clustering) step-by-step in a easy and clear means. You’ll not solely perceive what Varclus is, but in addition easy methods to interpret it. Plus, we’ll dive right into a hands-on instance utilizing Excel to search out Varclus for pattern information.
Variable clustering (Varclus) is a method utilized in multivariate statistics to group variables into clusters primarily based on their similarities. This method is commonly used for variable/function discount
Under are the Primary steps for calculating Varclus. I’ll present every step with an instance in an in depth means beneath
1. Calculate Correlation Matrix
2. Preliminary Clustering
3. Resolve the Variety of Clusters
4. Calculate Rsquare
Right here’s a breakdown of every step that can assist you perceive Varclus higher. To observe alongside, I’ve created a pattern dataset with 6 columns and 6 rows. You possibly can entry this information utilizing the beneath hyperlink. Ideally, strive opening the spreadsheet beneath utilizing MS Excel.
Step 1: Calculate Correlation Matrix
To evaluate the similarity between variables in our dataset, we are able to calculate a correlation matrix. This matrix reveals the correlation coefficient between every pair of variables. A correlation coefficient nearer to 1 signifies a powerful constructive relationship, whereas a worth nearer to -1 signifies a powerful detrimental relationship. We are able to use the CORREL perform in Excel to calculate these coefficients. As an example, the correlation between Hours_of_Study (column C) and Scholar(column B) will be discovered utilizing the method: =CORREL($B$2:$B$7,C2:C7)
Step 2: Preliminary Clustering
Clustering is a strong machine-learning approach that teams related information factors collectively primarily based on their traits. Its purpose is to prepare information into clusters the place factors inside a cluster share extra similarities with one another in comparison with factors in several clusters. There are numerous clustering algorithms accessible, however for now, let’s give attention to Hierarchical Clustering.
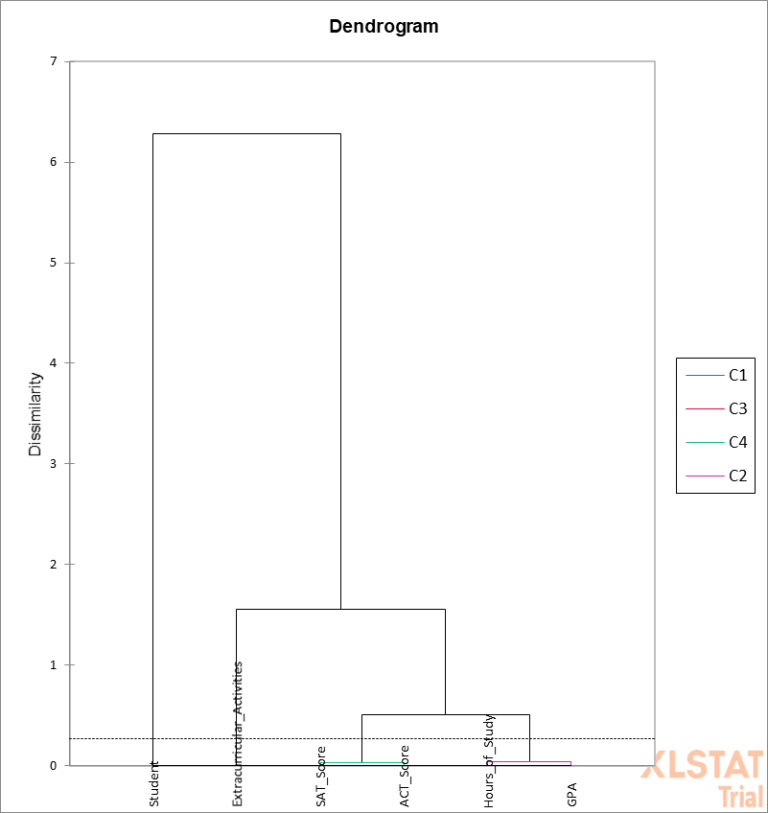
Whereas Microsoft Excel doesn’t supply built-in performance for Hierarchical Clustering, I’ve used the XLSTAT add-on to carry out this evaluation within the connected Excel sheet. The ensuing dendrogram, which is a tree-like construction, visually represents the hierarchical relationships between the info factors.
A dendrogram plot is a visible illustration of hierarchical clustering that reveals the association of clusters shaped at every step of the algorithm. Right here’s a brief interpretation of a dendrogram plot and what the peak of the tree represents:
Dendrogram Interpretation:
- Peak of the Tree: The peak at which two branches merge represents the gap or dissimilarity between the clusters being joined. A decrease peak means the clusters are extra related, whereas the next peak signifies larger dissimilarity.
- Chopping the Dendrogram: By drawing a horizontal line throughout the dendrogram at a selected peak, you may decide the variety of clusters. The variety of vertical traces intersected by the horizontal line signifies the variety of clusters at that dissimilarity degree.
Step 3: Resolve the variety of clusters
XLSTAT presents an preliminary suggestion for the optimum variety of clusters primarily based on the dendrogram’s construction and the variety of clusters themselves. Nonetheless, we are able to additionally leverage the dendrogram to outline our personal cluster boundaries visually. On this case, we’ll settle for XLSTAT’s suggestion of 4 clusters:
Right here now we have 4 clusters
Cluster 1: GPA and Hours_of_Study
Cluster 2: SAT_score and ACT_score
Cluster 3: Extracurricular Actions
Cluster 4: Scholar
One solution to summarize the values inside every cluster is by calculating the typical of the variable values. This would offer a central tendency for every cluster. Under are the cluster values
Step 4: Calculate Rsquare
As a result of variables inside the similar cluster are correlated, we would need to choose a single consultant variable from every cluster. This consultant variable ought to ideally be extremely correlated with different variables in its personal cluster (centroid) and have a weak correlation with the variables within the nearest neighboring cluster.
One solution to determine such a consultant variable is by calculating the R-squared worth. R-squared represents the proportion of variance in a single variable defined by one other variable. We are able to calculate the R-squared worth between a variable and its personal cluster (centroid) and the R-squared worth between the identical variable and the closest neighboring cluster.
The variable with a excessive R-squared worth for its personal cluster and a low R-squared worth for the closest neighboring cluster is an efficient candidate for the consultant variable.
Right here’s the method for calculating R-squared
Step 4.1 Calculating the closest cluster
Earlier than calculating the R-squared values, we have to decide the closest cluster for every cluster in our evaluation. Euclidean distance is a typical technique for measuring the similarity between information factors.
Within the context of Varclus, we are able to calculate the Euclidean distance between the centroids (consultant factors) of every cluster. The cluster with the smallest Euclidean distance to a given cluster is taken into account its nearest neighbor.
Step 4.2 Calculating R Sq.
Fortunately, Excel presents a handy perform named “RSQ” to calculate R-squared values. We are able to leverage this perform to compute the R-squared worth between every variable and its personal cluster centroid (heart) in addition to the R-squared worth between the identical variable and the closest neighboring cluster
Step 4.3 Calculating 1- R Squared Ratio
Recall that we’re aiming to pick out a consultant variable for every cluster. This variable needs to be extremely correlated with the opposite variables in its personal cluster (centroid) and weakly correlated with the variables within the nearest neighboring cluster.
To determine such a variable, we are able to make the most of the 1-R-squared ratio. A variable with the bottom 1-R-squared ratio is more likely to be a very good consultant for the cluster. It means most correlation with personal cluster and minimal correlation with subsequent cluster
By analyzing the 1-R-squared ratios, we are able to see that inside cluster 1, GPA has a stronger correlation with the opposite variables within the cluster in comparison with Hours_of_Study. This means that GPA is extra consultant of the commonalities inside cluster 1 and reveals a weaker relationship with the variables within the nearest neighboring cluster. Due to this fact, primarily based on this evaluation, we are able to select GPA because the consultant variable for cluster 1, successfully decreasing the variety of variables from two to 1.
Notes
A typical query that arises is why we haven’t used Principal Element Evaluation (PCA) on this clarification of Varclus. Whereas PCA generally is a useful device for dimensionality discount, it’s vital to notice that it’s an non-compulsory step within the Varclus course of. Moreover, understanding how Varclus works along with PCA will be extra complicated.
Remark in case of any doubts, and I’ll attempt to reply ASAP.
Thanks for Studying.
Venkat Sai