Optimization capabilities are the spine of coaching neural networks. They information the method of minimizing the loss perform, permitting fashions to make correct predictions. Amongst these, gradient descent and its variants are a number of the most basic strategies. Let’s take a deep dive into these ideas, exploring again propagation, reminiscence footprint, and the intricacies of gradient descent.
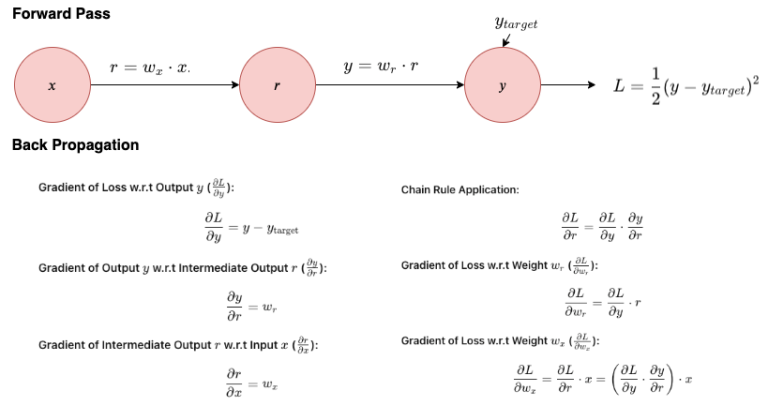
Again propagation is the basic algorithm underlying most neural community coaching. It minimizes the loss perform by updating the mannequin’s weights and biases to scale back the error between the mannequin’s predictions and the precise knowledge. Right here’s the way it works:
Ahead Move:
- The enter knowledge is handed by way of the community layer by layer (from the enter layer to the output layer) utilizing the present weights and biases.
- The ultimate output is in contrast with the true worth to calculate the loss utilizing a particular loss perform.
Backward Move:
- The gradient of the loss perform is calculated with respect to every weight and bias by making use of the chain rule of calculus, usually achieved layer by layer in reverse (from the output again to the enter).
- These gradients point out how a lot a small change in every weight and bias would change the loss.
Replace Parameters:
- The weights and biases are up to date utilizing the gradients computed through the again propagation, sometimes utilizing an optimization algorithm like Gradient Descent (GD), Stochastic Gradient Descent (SGD) or its variants (Adam, RMSprop, and so on.).
- The replace usually seems like this: weight=weight−η⋅gradient, the place η is the educational charge.
Iterate:
- This course of is repeated for a lot of iterations (epochs) over the coaching dataset till the loss reaches a minimal or till different stopping standards are met.
The reminiscence footprint of again propagation is essential, particularly when coaching massive fashions or coping with massive datasets. Right here’s what contributes to reminiscence use throughout again propagation:
Storage of Weights and Biases: Every parameter (weight and bias) of the community have to be saved.
Activation Values: The output of every neuron (after making use of the activation perform) in every layer have to be saved to be used through the backward move.
Gradients: The gradients of the loss with respect to every parameter are computed and saved through the backward move.
Intermediate Variables: Relying on the complexity of the layers and operations (like batch normalization, dropout, and so on.), intermediate variables could have to be saved.
Rely Whole Parameters: Calculate the full variety of trainable parameters (weights and biases). Every parameter sometimes requires 4 bytes of reminiscence if utilizing 32-bit floating-point illustration.
Account for Activations: Multiply the variety of neurons in every layer by the dimensions of the information sort used (e.g., 4 bytes for 32-bit float) to get the reminiscence required for activations. Bear in mind, activations have to be saved for every layer.
Take into account Batch Measurement: The reminiscence required will increase with the batch measurement since activations and gradients for every occasion within the batch have to be saved concurrently.
Sum Up Every little thing: Whole reminiscence = Reminiscence for parameters + Reminiscence for activations + Reminiscence for gradients.
Instance Calculation
Suppose a easy community with:
- An enter layer of 784 items (for MNIST photos), one hidden layer of 128 items, and an output layer of 10 items.
- Weights and biases for every layer, activations at every layer, and gradients to be saved.
Calculation:
- Weights and Biases: (784 × 128 + 128) + (128 × 10 + 10) parameters.
- Activations: For a batch measurement of 64, (64 × [784 + 128 + 10]) activations.
- Every worth saved as a 32-bit float (4 bytes).
The overall reminiscence footprint would then be calculated by multiplying the full depend of things needing storage (parameters, activations for every merchandise within the batch, and gradients) by the reminiscence required per merchandise.
What’s within the Reminiscence?
- Mannequin parameters (weights and biases) and their gradients.
- Activation values for every layer for every coaching instance within the batch.
- Short-term variables relying on the particular operations and layers used within the mannequin.
Managing reminiscence effectively is essential in coaching bigger fashions or utilizing limited-resource environments. Strategies like decreased precision arithmetic (e.g., 16-bit floats), utilizing environment friendly batch sizes, or gradient checkpointing (storing solely sure layer activations and recomputing others as wanted through the backward move) may help scale back the reminiscence footprint.
The load replace processes in logistic regression and neural networks are each primarily based on optimization and gradient descent, however differ because of their architectural complexities. Right here’s a concise comparability:
Logistic Regression Weight Replace
Mannequin Construction:
- Single-layer mannequin with out hidden layers, utilizing a sigmoid perform.
Loss Operate:
- Binary cross-entropy loss.
Gradient Calculation:
- Derived from the sigmoid perform; entails the distinction between predicted chances and precise labels, multiplied by enter options.
Weight Replace Rule:
- Weights are up to date as: weight=weight−η⋅gradient the place η is the educational charge.
Neural Community Weight Replace
Mannequin Construction:
- A number of layer mannequin together with hidden layers with activation capabilities that may introduce non-linearities, making the mannequin able to studying extra complicated patterns than logistic regression.
Loss Operate:
- Varies by job: binary cross-entropy, categorical cross-entropy, imply squared error, and so on.
Gradient Calculation (Again propagation):
- Gradients are computed by way of again propagation, layer by layer, utilizing the chain rule. This entails extra complicated calculations because of a number of layers and activation capabilities.
Weight Replace Rule:
- Comparable type to logistic regression: Weights are up to date as: weight=weight−η⋅gradient the place η is the educational charge.
- Makes use of superior optimizers like SGD with momentum, Adam, or RMSprop to regulate the educational charge dynamically and enhance convergence.
Regardless of their shared basis in gradient descent, logistic regression and neural networks differ considerably of their weight replace mechanisms as a result of complexity and depth of neural community architectures.
Key Variations
- Complexity of Gradient Calculation: Logistic regression entails a simple gradient calculation, whereas neural networks require a posh, layer-wise again propagation algorithm to compute gradients.
- Depth and Non-linearity: Neural networks make the most of a number of layers and non-linear activation capabilities, which might seize deeper and extra complicated relationships within the knowledge in comparison with the only linear boundary discovered by logistic regression.
- Optimization Strategies: Whereas each could use primary gradient descent, neural networks usually profit from superior optimizers that deal with points like various studying charges, native minima, or saddle factors extra successfully.
Convex Operate:
Think about a easy, U-shaped bowl. For those who begin at any level on the sting of this bowl and transfer downward, you’ll at all times head in direction of the bottom level on the backside. Mathematically, a convex perform has a single world minimal and no native minima. The gradient (slope) at all times factors in direction of this world minimal.
Concave Operate:
That is the alternative, like an upside-down U-shaped dome. Right here, we’re interested by maximization, however for minimization issues, we often cope with convex capabilities.
Gradient Descent and Derivatives
- Gradient Descent: This algorithm helps discover the minimal of a perform. It really works by calculating the gradient (slope) of the perform on the present level after which shifting in the other way of the gradient. The dimensions of the steps taken is managed by the educational charge.
- Spinoff: The by-product of a perform at some extent tells you the slope or charge of change of the perform at that time. For gradient descent, the by-product helps decide the course and magnitude of the steps taken in direction of the minimal.
Dataset and Mannequin Complexities
Easy datasets and easy fashions:
Easy datasets have clear, simply identifiable patterns and relationships between options and the goal variable. For instance, a dataset the place the connection between variables is linear and there’s little noise. The loss perform for fashions skilled on such datasets is usually convex, resembling a easy, bowl-shaped curve. This makes it simpler for gradient descent to seek out the worldwide minimal. Easy fashions like linear regression or logistic regression are comparatively easy and are appropriate for less complicated datasets. The loss surfaces for these fashions are typically convex, facilitating the discovering of the worldwide minimal.
Advanced datasets and complicated fashions:
Advanced datasets have intricate, non-linear relationships and probably a number of noise. Excessive-dimensional knowledge with many options may add complexity. The loss perform for these datasets is non-convex, with many peaks and valleys, making the optimization panorama rugged. Right here, gradient descent can simply get caught in native minima. Deep neural networks or fashions with many parameters are complicated and may seize intricate patterns within the knowledge. Nevertheless, their loss surfaces are non-convex, filled with native minima and saddle factors (flat areas which are neither minima nor maxima), complicating the optimization course of.
To cope with the challenges posed by non-convex loss landscapes:
- A number of Runs: Run gradient descent a number of instances with completely different beginning factors to extend the possibilities of discovering the worldwide minimal.
- Momentum: Use momentum in gradient descent to assist the algorithm push by way of native minima.
- Adaptive Studying Charges: Use optimizers like Adam or RMSprop that modify the educational charge throughout coaching.
- Stochastic Gradient Descent (SGD): Introduce randomness by utilizing mini-batches of information, which may help the algorithm escape native minima.
Understanding convex and non-convex landscapes, and the ideas of native and world minima, is essential in machine studying. The complexity of the dataset and mannequin determines the form of the loss perform and the challenges confronted throughout optimization. Superior strategies and methods may help navigate these challenges, bettering the possibilities of discovering the very best resolution.