Positive, I might help you with that. Let’s begin by creating random information after which we’ll construct a polynomial regression mannequin utilizing Python. Right here’s the plan:
- Generate Random Knowledge: We’ll generate a set of random information factors that observe a polynomial relationship.
- Match Polynomial Regression Mannequin: We’ll match a polynomial regression mannequin to this information.
- Visualize the Outcomes: We’ll visualize the unique information factors and the fitted polynomial curve.
Let’s start by producing the random information.
We’ll create a dataset the place y is a polynomial operate of x with some added random noise. For simplicity, let’s use a quadratic operate (second-degree polynomial) as our base operate.
We’ll use the numpy and scikit-learn libraries to suit a polynomial regression mannequin.
We’ll use matplotlib to visualise the info and the fitted polynomial curve.
Right here is the whole code to carry out these steps
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline# Step 1: Generate random information
np.random.seed(0) # For reproducibility
x = np.random.rand(100, 1) * 10 # Random x values in vary [0, 10]
y = 2 + 3 * x + x**2 + np.random.randn(100, 1) * 10 # Quadratic relationship with noise
# Step 2: Match polynomial regression mannequin
diploma = 2 # Diploma of the polynomial
polyreg = make_pipeline(PolynomialFeatures(diploma), LinearRegression())
polyreg.match(x, y)
y_pred = polyreg.predict(x)
# Step 3: Visualize the outcomes
plt.scatter(x, y, coloration='blue', label='Knowledge Factors')
plt.plot(np.kind(x, axis=0), np.kind(y_pred, axis=0), coloration='pink', label='Polynomial Match')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Polynomial Regression (Diploma 2)')
plt.legend()
plt.present()
- Knowledge Era:
- We generate 100 random
xvalues between 0 and 10. - The corresponding
yvalues are generated utilizing a quadratic operatey = 2 + 3 * x + x**2with added Gaussian noise.
2. Polynomial Regression:
- We use
PolynomialFeaturesfromscikit-learnto rework our options into polynomial options. - We create a pipeline that first transforms the info into polynomial options after which applies linear regression.
- We match this mannequin to our information.
3. Visualization:
- We plot the unique information factors.
- We plot the polynomial regression curve utilizing the fitted mannequin.
Let’s execute the code and visualize the outcomes. I’ll run the code within the subsequent step.
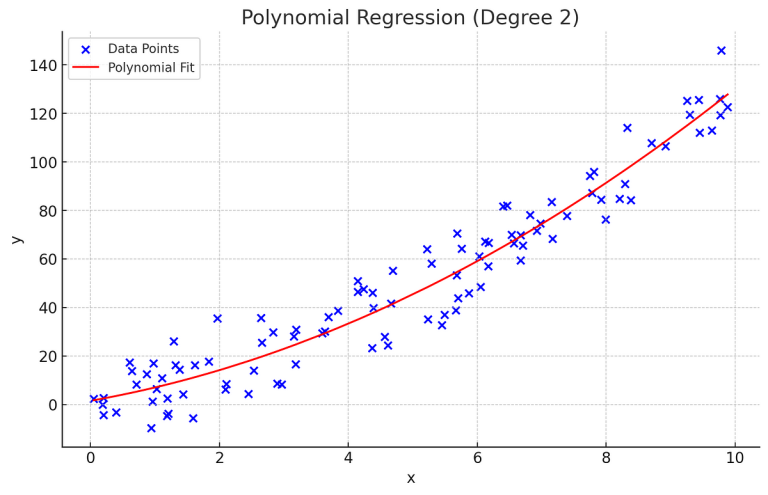
Right here is the generated plot displaying the polynomial regression outcomes:
- Blue dots symbolize the unique information factors.
- Pink curve represents the fitted polynomial regression mannequin (diploma 2).
As we are able to see, the pink curve suits the quadratic development within the information fairly nicely, indicating that our polynomial regression mannequin has efficiently captured the underlying relationship between x and y. You probably have some other questions or want additional changes, be happy to ask!